What waves know about their surroundings
- Photo: TU Wien: What waves know about their surroundings.
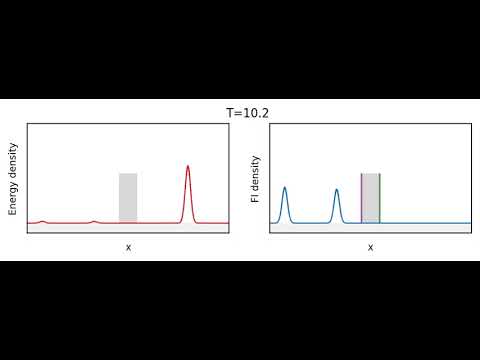
- Video: TU Wien TV: Was Wellen über ihre Umgebung wissen - A one-dimensional wave packet like a pulse of light enters the system from the left and hits a barrier at T=6 (see left panel). The interaction between the wave packet and the sides of the barrier results in the creation of Fisher Information (see right panel). While almost all of the energy is transmitted to the right, all of the information is reflected back to the left.
Waves pick up information from their environment through which they propagate. A theory of information carried by waves has now been developed at TU Wien – with astonishing results that can be utilised for technical applications.
We use ultrasound to analyse the body, radar systems to study airspace or seismic waves to study the interior of our planet. Many areas of research are dealing with waves that are deflected, scattered or reflected by their surroundings. As a result, these waves carry a certain amount of information about their environment, and this information must then be extracted as comprehensively and precisely as possible.
Searching for the best way to do this has been the subject of research around the world for many years. TU Wien has now succeeded in describing the information carried by a wave about its environment with mathematical precision. This has made it possible to show how waves pick up information about an object and then transport it to a measuring device. This can now be used to generate customised waves to extract the maximum amount of information from the environment - for more precise imaging processes, for example. This theory was confirmed with microwave experiments. The results were published in the journal ‘Nature Physics’.
 TU Wien: What waves know about their surroundings - Teflon objects (orange cylinders) were placed in a waveguide with a rectangular cross-section. Then, an electromagnetic signal (blue wavefront) was injected from the right to extract information about the metallic cuboid shown in gray. By measuring the wave field in the area indicated in red, the researchers could show how information is generated and transported by an electromagnetic signal. For example, the flow of information about the horizontal position of the cuboid is shown in the inset at the bottom right (blue arrows). One sees that information is generated on the cuboid's right-hand side and then transported to the right towards the opening of the waveguide.
TU Wien: What waves know about their surroundings - Teflon objects (orange cylinders) were placed in a waveguide with a rectangular cross-section. Then, an electromagnetic signal (blue wavefront) was injected from the right to extract information about the metallic cuboid shown in gray. By measuring the wave field in the area indicated in red, the researchers could show how information is generated and transported by an electromagnetic signal. For example, the flow of information about the horizontal position of the cuboid is shown in the inset at the bottom right (blue arrows). One sees that information is generated on the cuboid's right-hand side and then transported to the right towards the opening of the waveguide.
Where exactly is the information located?
“The basic idea is quite simple: you send a wave at an object and the part of the wave that is scattered back from the object is measured by a detector,” says Prof Stefan Rotter from the Institute of Theoretical Physics at TU Wien. “The data can then be used to learn something about the object – for example, its precise position, speed or size.” This information about the environment that this wave carries with it is known as ‘Fisher information’.
However, it is often not possible to capture the entire wave. Usually, only part of the wave reaches the detector. This raises the question: Where exactly is this information actually located in the wave? Are there parts of the wave that can be safely ignored? Would a different waveform perhaps provide more information to the detector?
“To get to the bottom of these questions, we took a closer look at the mathematical properties of this Fisher information and came up with some astonishing results,” says Stefan Rotter. “The information fulfils a so-called continuity equation – the information in the wave is preserved as it moves through space, according to laws which are very similar laws to the conservation of energy, for example.”
A comprehensible path of information
Using the newly developed formalism, the research team has now been able to calculate exactly at which point in space the wave actually carries how much information about the object. It turns out that the information about different properties of the object (such as position, speed and size) can be hidden in completely different parts of the wave.
As the theoretical calculations show, the information content of the wave depends precisely on how strongly the wave is influenced by certain properties of the object under investigation. “For example, if we want to measure whether an object is a little further to the left or a little further to the right, then the Fisher information is carried precisely by the part of the wave that comes into contact with the right and left edges of the object,” says Jakob Hüpfl, the doctoral student who played a key role in the study. “This information then spreads out, and the more of this information reaches the detector, the more precisely the position of the object can be read from it.”
Microwave experiments confirm the theory
In Ulrich Kuhl's group at the University of Cote d'Azur in Nice, experiments were carried out by Felix Russo as part of his master's thesis: A disordered environment was created in a microwave chamber using randomly positioned Teflon objects. Between these objects, a metallic rectangle was placed whose position was to be determined. Microwaves were sent through the system and then picked up by a detector. The question now was: How well can the position of the metal rectangle be deduced from the waves caught in the detector in such a complicated physical situation and how does the information flow from the rectangle to the detector?
By precisely measuring the microwave field, it was possible to show exactly how the information about the horizontal and vertical position of the rectangle spreads: it emanates from the respective edges of the rectangle and then moves along with the wave – without any information being lost, just as predicted by the newly developed theory.
 TU Wien: What waves know about their surroundings - Experimental setup to measure the information transport via microwaves at Université Côte d’Azur. (Nice). On the table, one can see a waveguide into which an electromagnetic signal is injected (blue cables in the background). Inside the waveguide are Teflon objects (white cylinders in the foreground) that scatter the signal. This creates a complex wave field, which was measured at various points to determine the flow of information about the horizontal position of the metallic cuboid in the foreground.
TU Wien: What waves know about their surroundings - Experimental setup to measure the information transport via microwaves at Université Côte d’Azur. (Nice). On the table, one can see a waveguide into which an electromagnetic signal is injected (blue cables in the background). Inside the waveguide are Teflon objects (white cylinders in the foreground) that scatter the signal. This creates a complex wave field, which was measured at various points to determine the flow of information about the horizontal position of the metallic cuboid in the foreground.
Possible applications in many areas
“This new mathematical description of Fisher information has the potential to improve the quality of a variety of imaging methods,” says Stefan Rotter. If it is possible to quantify where the desired information is located and how it propagates, then it also becomes possible, for example, to position the detector more appropriately or to calculate customised waves that transport the maximum amount of information to the detector.
“We tested our theory with microwaves, but it is equally valid for a wide variety of waves with different wavelengths,” emphasises Rotter. “We provide simple formulas that can be used to improve microscopy methods as well as quantum sensors.“